Projects
List by topic of recent works I have been involved in.
Spectral Methods for Uncertainty Quantification Problems
Sensitivity Analysis and Variance Decomposition for Stochastic Systems
Bayesian Inference
Optimization under Uncertainty
Scientific Computing and HPC
Spectral Methods for Uncertainty Quantification Problems
This activity concerns methodological advances on Uncertainty Quantification and Sensitivity Analysis methods using Polynomial Chaos and Stochastic Spectral expansions. Our efforts have mostly been dedicated to the improvement of non-intrusive methods: adaptive pseudo spectral projection, preconditioning, Bayesian estimation of the projection coefficients, reduction strategies,...
On few specific problems, we have also pursued the improvement and complexity reduction of the Galerkin approach: the Galerkin approximation of stochastic periodic dynamics and the application of the Proper Generalized Decomposition method to the steady Navier-Stokes equations.
On few specific problems, we have also pursued the improvement and complexity reduction of the Galerkin approach: the Galerkin approximation of stochastic periodic dynamics and the application of the Proper Generalized Decomposition method to the steady Navier-Stokes equations.
Non-Intrusive spectral methods
Sparse Pseudo Spectral Projection Methods with Directional Adaptation for Uncertainty Quantification.
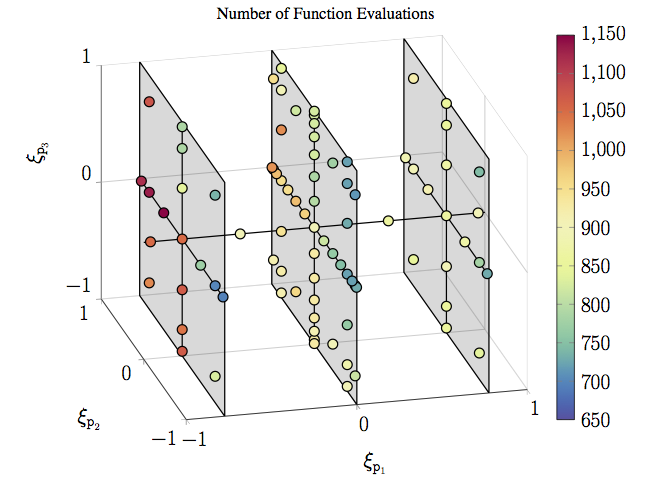 We investigate two methods to build a polynomial approximation of a model output depending on some parameters. The two approaches are based on pseudo-spectral projection (PSP) methods on adaptively constructed sparse grids, and aim at providing a finer control of the resolution along two distinct subsets of model parameters. The control of the error along different subsets of parameters may be needed for instance in the case of a model depending on uncertain parameters and deterministic design variables. We first consider a nested approach where an independent adaptive sparse grid PSP is performed along the first set of directions only, and at each point a sparse grid is constructed adaptively in the second set of directions. We then consider the application of aPSP in the space of all parameters, and introduce directional refinement criteria to provide a tighter control of the projection error along individual dimensions. Specifically, we use a Sobol decomposition of the projection surpluses to tune the sparse grid adaptation. The behavior and performance of the two approaches are compared for a simple two-dimensional test problem and for a shock-tube ignition model involving 22 uncertain parameters and 3 design parameters. The numerical experiments indicate that whereas both methods provide effective means for tuning the quality of the representation along distinct subsets of parameters, PSP in the global parameter space generally requires fewer model evaluations than the nested approach to achieve similar projection error. In addition, the global approach is better suited for generalization to more than two subsets of directions.
We investigate two methods to build a polynomial approximation of a model output depending on some parameters. The two approaches are based on pseudo-spectral projection (PSP) methods on adaptively constructed sparse grids, and aim at providing a finer control of the resolution along two distinct subsets of model parameters. The control of the error along different subsets of parameters may be needed for instance in the case of a model depending on uncertain parameters and deterministic design variables. We first consider a nested approach where an independent adaptive sparse grid PSP is performed along the first set of directions only, and at each point a sparse grid is constructed adaptively in the second set of directions. We then consider the application of aPSP in the space of all parameters, and introduce directional refinement criteria to provide a tighter control of the projection error along individual dimensions. Specifically, we use a Sobol decomposition of the projection surpluses to tune the sparse grid adaptation. The behavior and performance of the two approaches are compared for a simple two-dimensional test problem and for a shock-tube ignition model involving 22 uncertain parameters and 3 design parameters. The numerical experiments indicate that whereas both methods provide effective means for tuning the quality of the representation along distinct subsets of parameters, PSP in the global parameter space generally requires fewer model evaluations than the nested approach to achieve similar projection error. In addition, the global approach is better suited for generalization to more than two subsets of directions.
 We investigate two methods to build a polynomial approximation of a model output depending on some parameters. The two approaches are based on pseudo-spectral projection (PSP) methods on adaptively constructed sparse grids, and aim at providing a finer control of the resolution along two distinct subsets of model parameters. The control of the error along different subsets of parameters may be needed for instance in the case of a model depending on uncertain parameters and deterministic design variables. We first consider a nested approach where an independent adaptive sparse grid PSP is performed along the first set of directions only, and at each point a sparse grid is constructed adaptively in the second set of directions. We then consider the application of aPSP in the space of all parameters, and introduce directional refinement criteria to provide a tighter control of the projection error along individual dimensions. Specifically, we use a Sobol decomposition of the projection surpluses to tune the sparse grid adaptation. The behavior and performance of the two approaches are compared for a simple two-dimensional test problem and for a shock-tube ignition model involving 22 uncertain parameters and 3 design parameters. The numerical experiments indicate that whereas both methods provide effective means for tuning the quality of the representation along distinct subsets of parameters, PSP in the global parameter space generally requires fewer model evaluations than the nested approach to achieve similar projection error. In addition, the global approach is better suited for generalization to more than two subsets of directions.
We investigate two methods to build a polynomial approximation of a model output depending on some parameters. The two approaches are based on pseudo-spectral projection (PSP) methods on adaptively constructed sparse grids, and aim at providing a finer control of the resolution along two distinct subsets of model parameters. The control of the error along different subsets of parameters may be needed for instance in the case of a model depending on uncertain parameters and deterministic design variables. We first consider a nested approach where an independent adaptive sparse grid PSP is performed along the first set of directions only, and at each point a sparse grid is constructed adaptively in the second set of directions. We then consider the application of aPSP in the space of all parameters, and introduce directional refinement criteria to provide a tighter control of the projection error along individual dimensions. Specifically, we use a Sobol decomposition of the projection surpluses to tune the sparse grid adaptation. The behavior and performance of the two approaches are compared for a simple two-dimensional test problem and for a shock-tube ignition model involving 22 uncertain parameters and 3 design parameters. The numerical experiments indicate that whereas both methods provide effective means for tuning the quality of the representation along distinct subsets of parameters, PSP in the global parameter space generally requires fewer model evaluations than the nested approach to achieve similar projection error. In addition, the global approach is better suited for generalization to more than two subsets of directions.
Preconditioned Bayesian Regression for Stochastic Chemical Kinetics.
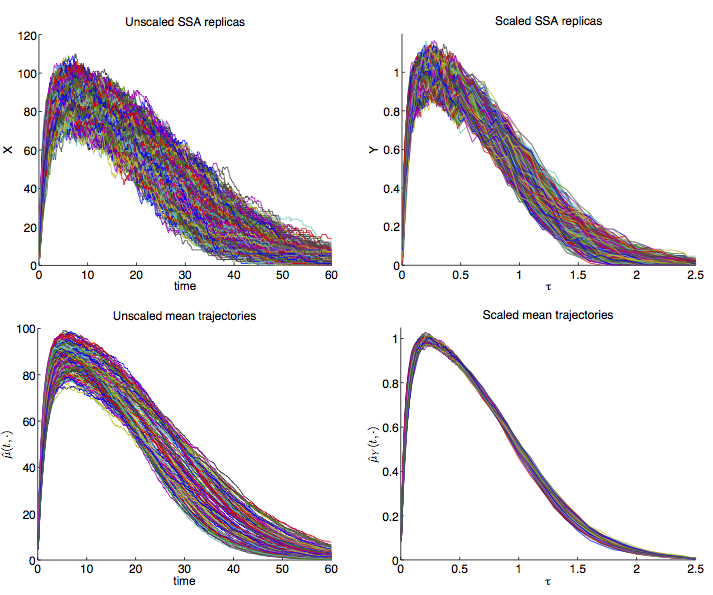 We develop a preconditioned Bayesian regression method that enables sparse polynomial chaos representations of noisy outputs for stochastic chemical systems with uncertain reaction rates. The approach is based on the definition of an appropriate multiscale transformation of the state variables coupled with a Bayesian regression formalism. This enables efficient and robust recovery of both the transient dynamics and the corresponding noise levels. Implementation of the present approach is illustrated through applications to a stochastic Michaelis--Menten dynamics and a higher dimensional example involving a genetic positive feedback loop. In all cases, a stochastic simulation algorithm (SSA) is used to compute the system dynamics. Numerical experiments show that Bayesian preconditioning algorithms can simultaneously accommodate large noise levels and large variability with uncertain parameters, and that robust estimates can be obtained with a small number of SSA realizations.
We develop a preconditioned Bayesian regression method that enables sparse polynomial chaos representations of noisy outputs for stochastic chemical systems with uncertain reaction rates. The approach is based on the definition of an appropriate multiscale transformation of the state variables coupled with a Bayesian regression formalism. This enables efficient and robust recovery of both the transient dynamics and the corresponding noise levels. Implementation of the present approach is illustrated through applications to a stochastic Michaelis--Menten dynamics and a higher dimensional example involving a genetic positive feedback loop. In all cases, a stochastic simulation algorithm (SSA) is used to compute the system dynamics. Numerical experiments show that Bayesian preconditioning algorithms can simultaneously accommodate large noise levels and large variability with uncertain parameters, and that robust estimates can be obtained with a small number of SSA realizations.
 We develop a preconditioned Bayesian regression method that enables sparse polynomial chaos representations of noisy outputs for stochastic chemical systems with uncertain reaction rates. The approach is based on the definition of an appropriate multiscale transformation of the state variables coupled with a Bayesian regression formalism. This enables efficient and robust recovery of both the transient dynamics and the corresponding noise levels. Implementation of the present approach is illustrated through applications to a stochastic Michaelis--Menten dynamics and a higher dimensional example involving a genetic positive feedback loop. In all cases, a stochastic simulation algorithm (SSA) is used to compute the system dynamics. Numerical experiments show that Bayesian preconditioning algorithms can simultaneously accommodate large noise levels and large variability with uncertain parameters, and that robust estimates can be obtained with a small number of SSA realizations.
We develop a preconditioned Bayesian regression method that enables sparse polynomial chaos representations of noisy outputs for stochastic chemical systems with uncertain reaction rates. The approach is based on the definition of an appropriate multiscale transformation of the state variables coupled with a Bayesian regression formalism. This enables efficient and robust recovery of both the transient dynamics and the corresponding noise levels. Implementation of the present approach is illustrated through applications to a stochastic Michaelis--Menten dynamics and a higher dimensional example involving a genetic positive feedback loop. In all cases, a stochastic simulation algorithm (SSA) is used to compute the system dynamics. Numerical experiments show that Bayesian preconditioning algorithms can simultaneously accommodate large noise levels and large variability with uncertain parameters, and that robust estimates can be obtained with a small number of SSA realizations.
Galerkin projection methods
Model Reduction Based on Proper Generalized Decomposition for the Stochastic Steady Incompressible Navier--Stokes Equations.
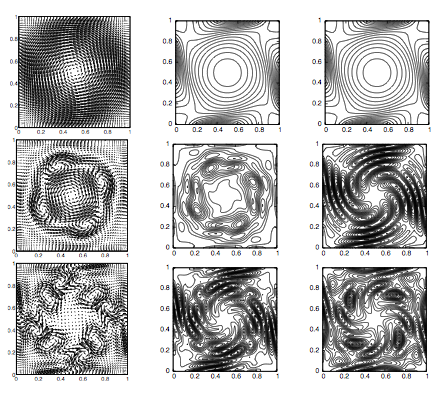 In this paper we consider a Proper Generalized Decomposition method to solve the steady incompressible Navier–Stokes equations with random Reynolds number and forcing term. The aim of such technique is to compute a low-cost reduced basis approximation of the full Stochastic Galerkin solution of the problem at hand. A particular algorithm, inspired by the Arnoldi method for solving eigenproblems, is proposed for an efficient greedy construction of a deterministic reduced basis approximation. This algorithm decouples the computation of the deterministic and stochastic components of the solution, thus allowing reuse of preexisting deterministic Navier–Stokes solvers. It has the remarkable property of only requiring the solution of $m$ uncoupled deterministic problems for the construction of a $m$-dimensional reduced basis rather than $M$ coupled problems of the full Stochastic Galerkin approximation space, with $m\ll M$ (up to one order of magnitude for the problem at hand in this work).
In this paper we consider a Proper Generalized Decomposition method to solve the steady incompressible Navier–Stokes equations with random Reynolds number and forcing term. The aim of such technique is to compute a low-cost reduced basis approximation of the full Stochastic Galerkin solution of the problem at hand. A particular algorithm, inspired by the Arnoldi method for solving eigenproblems, is proposed for an efficient greedy construction of a deterministic reduced basis approximation. This algorithm decouples the computation of the deterministic and stochastic components of the solution, thus allowing reuse of preexisting deterministic Navier–Stokes solvers. It has the remarkable property of only requiring the solution of $m$ uncoupled deterministic problems for the construction of a $m$-dimensional reduced basis rather than $M$ coupled problems of the full Stochastic Galerkin approximation space, with $m\ll M$ (up to one order of magnitude for the problem at hand in this work).
 In this paper we consider a Proper Generalized Decomposition method to solve the steady incompressible Navier–Stokes equations with random Reynolds number and forcing term. The aim of such technique is to compute a low-cost reduced basis approximation of the full Stochastic Galerkin solution of the problem at hand. A particular algorithm, inspired by the Arnoldi method for solving eigenproblems, is proposed for an efficient greedy construction of a deterministic reduced basis approximation. This algorithm decouples the computation of the deterministic and stochastic components of the solution, thus allowing reuse of preexisting deterministic Navier–Stokes solvers. It has the remarkable property of only requiring the solution of $m$ uncoupled deterministic problems for the construction of a $m$-dimensional reduced basis rather than $M$ coupled problems of the full Stochastic Galerkin approximation space, with $m\ll M$ (up to one order of magnitude for the problem at hand in this work).
In this paper we consider a Proper Generalized Decomposition method to solve the steady incompressible Navier–Stokes equations with random Reynolds number and forcing term. The aim of such technique is to compute a low-cost reduced basis approximation of the full Stochastic Galerkin solution of the problem at hand. A particular algorithm, inspired by the Arnoldi method for solving eigenproblems, is proposed for an efficient greedy construction of a deterministic reduced basis approximation. This algorithm decouples the computation of the deterministic and stochastic components of the solution, thus allowing reuse of preexisting deterministic Navier–Stokes solvers. It has the remarkable property of only requiring the solution of $m$ uncoupled deterministic problems for the construction of a $m$-dimensional reduced basis rather than $M$ coupled problems of the full Stochastic Galerkin approximation space, with $m\ll M$ (up to one order of magnitude for the problem at hand in this work).
A Newton--Galerkin Method for Fluid Flow Exhibiting Uncertain Periodic Dynamics.
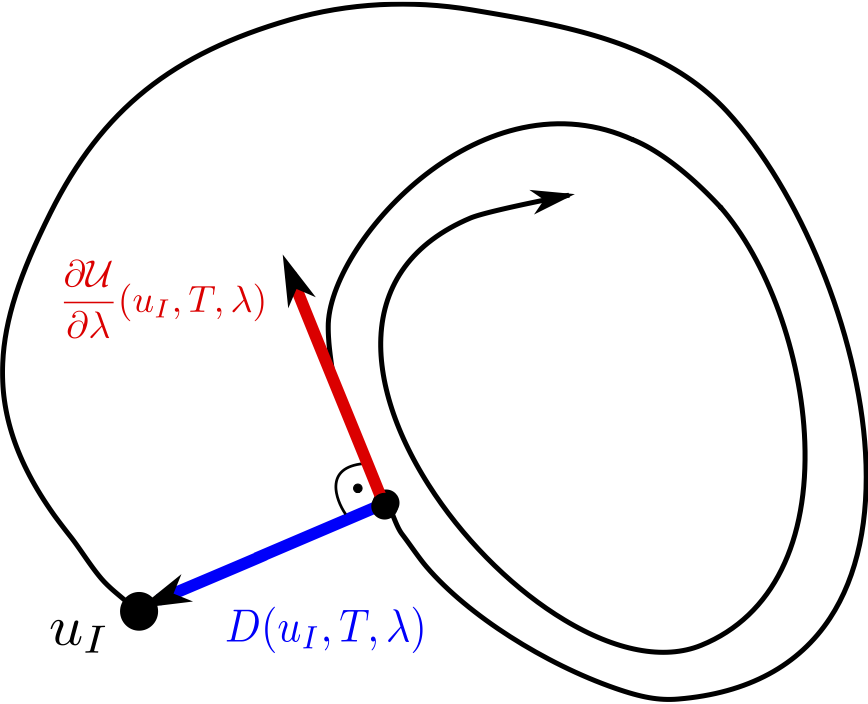 The determination of limit-cycles plays an important role in characterizing complex dynamical systems, such as unsteady fluid flows.
In practice, dynamical systems are described by models equations involving parameters which are seldom exactly known, leading to parametric uncertainties.
These parameters can be suitably modeled as random variables so, if the system possesses almost surely a stable time periodic solution, limit cycles become stochastic too.
This paper introduces a novel numerical method for the computation of stable stochastic limit-cycles based on the spectral stochastic finite element method with polynomial chaos (PC) expansions.
The method is designed to overcome the limitation of PC expansions related to convergence breakdown for long term integration.
First, a stochastic time scaling of the model equations is determined to control the phase-drift of the stochastic trajectories and allowing for accurate low order PC expansions.
Second, using the rescaled governing equations we aim at determining a stochastic initial condition and period such that the stochastic trajectories close after completion of one cycle.
The proposed method is implemented and demonstrated on a complex flow problem, modeled by the incompressible Navier-Stokes equations, consisting in the periodic vortex shedding behind a circular cylinder with stochastic inflow conditions.
Numerical results are verified by comparison to deterministic reference simulations and demonstrate high accuracy in capturing the stochastic variability of the limit-cycle with respect to the inflow parameters.
The determination of limit-cycles plays an important role in characterizing complex dynamical systems, such as unsteady fluid flows.
In practice, dynamical systems are described by models equations involving parameters which are seldom exactly known, leading to parametric uncertainties.
These parameters can be suitably modeled as random variables so, if the system possesses almost surely a stable time periodic solution, limit cycles become stochastic too.
This paper introduces a novel numerical method for the computation of stable stochastic limit-cycles based on the spectral stochastic finite element method with polynomial chaos (PC) expansions.
The method is designed to overcome the limitation of PC expansions related to convergence breakdown for long term integration.
First, a stochastic time scaling of the model equations is determined to control the phase-drift of the stochastic trajectories and allowing for accurate low order PC expansions.
Second, using the rescaled governing equations we aim at determining a stochastic initial condition and period such that the stochastic trajectories close after completion of one cycle.
The proposed method is implemented and demonstrated on a complex flow problem, modeled by the incompressible Navier-Stokes equations, consisting in the periodic vortex shedding behind a circular cylinder with stochastic inflow conditions.
Numerical results are verified by comparison to deterministic reference simulations and demonstrate high accuracy in capturing the stochastic variability of the limit-cycle with respect to the inflow parameters.
 The determination of limit-cycles plays an important role in characterizing complex dynamical systems, such as unsteady fluid flows.
In practice, dynamical systems are described by models equations involving parameters which are seldom exactly known, leading to parametric uncertainties.
These parameters can be suitably modeled as random variables so, if the system possesses almost surely a stable time periodic solution, limit cycles become stochastic too.
This paper introduces a novel numerical method for the computation of stable stochastic limit-cycles based on the spectral stochastic finite element method with polynomial chaos (PC) expansions.
The method is designed to overcome the limitation of PC expansions related to convergence breakdown for long term integration.
First, a stochastic time scaling of the model equations is determined to control the phase-drift of the stochastic trajectories and allowing for accurate low order PC expansions.
Second, using the rescaled governing equations we aim at determining a stochastic initial condition and period such that the stochastic trajectories close after completion of one cycle.
The proposed method is implemented and demonstrated on a complex flow problem, modeled by the incompressible Navier-Stokes equations, consisting in the periodic vortex shedding behind a circular cylinder with stochastic inflow conditions.
Numerical results are verified by comparison to deterministic reference simulations and demonstrate high accuracy in capturing the stochastic variability of the limit-cycle with respect to the inflow parameters.
The determination of limit-cycles plays an important role in characterizing complex dynamical systems, such as unsteady fluid flows.
In practice, dynamical systems are described by models equations involving parameters which are seldom exactly known, leading to parametric uncertainties.
These parameters can be suitably modeled as random variables so, if the system possesses almost surely a stable time periodic solution, limit cycles become stochastic too.
This paper introduces a novel numerical method for the computation of stable stochastic limit-cycles based on the spectral stochastic finite element method with polynomial chaos (PC) expansions.
The method is designed to overcome the limitation of PC expansions related to convergence breakdown for long term integration.
First, a stochastic time scaling of the model equations is determined to control the phase-drift of the stochastic trajectories and allowing for accurate low order PC expansions.
Second, using the rescaled governing equations we aim at determining a stochastic initial condition and period such that the stochastic trajectories close after completion of one cycle.
The proposed method is implemented and demonstrated on a complex flow problem, modeled by the incompressible Navier-Stokes equations, consisting in the periodic vortex shedding behind a circular cylinder with stochastic inflow conditions.
Numerical results are verified by comparison to deterministic reference simulations and demonstrate high accuracy in capturing the stochastic variability of the limit-cycle with respect to the inflow parameters.
Sensitivity Analysis and Variance Decomposition for Stochastic Systems
The modeling of complex systems often relies on stochastic approaches to account for unresolved sub-scale or unpredictable effects. Such models involve parameters, for instance fixing the magnitude of a noisy forcing, that must be calibrated to produce meaning full predictions. Quantifying the impact of parametric uncertainties in such systems is traditionally achieved by measuring the sensitivity of the stochastic output moments with respect to these parameters. However, moments-based sensitivity analysis involves an averaging step that amount to information loss.
For systems subjected to external noise, we have proposed a more complete characterization, efficiently separating the distinct contributions, to the overall variance, of the external noise, of the parametric uncertainty and of their interaction. The initial Galerkin approach has been recently extended to non-intrusive approaches to tackle the case of complex non-linear problems and the case of non-smooth quantities of interest.
Simulators with inherent stochastic dynamics (as opposed to subject of external noise) raise the issue of defining the conditional variances appearing in the decomposition. We proposed to identify the inherent stochasticity sources with the independent processes governing the reaction channels. It allowed us to measure the respective effects on the model output variance of different reaction channels. This idea was extended recently to incorporate additional parametric uncertainties.
These sensitivity analyses can be applied to a wide variety of models in many different application fields, ranging from climate modeling, finance, reactive systems, social networks, epidemic modeling, life sciences,...
For systems subjected to external noise, we have proposed a more complete characterization, efficiently separating the distinct contributions, to the overall variance, of the external noise, of the parametric uncertainty and of their interaction. The initial Galerkin approach has been recently extended to non-intrusive approaches to tackle the case of complex non-linear problems and the case of non-smooth quantities of interest.
Simulators with inherent stochastic dynamics (as opposed to subject of external noise) raise the issue of defining the conditional variances appearing in the decomposition. We proposed to identify the inherent stochasticity sources with the independent processes governing the reaction channels. It allowed us to measure the respective effects on the model output variance of different reaction channels. This idea was extended recently to incorporate additional parametric uncertainties.
These sensitivity analyses can be applied to a wide variety of models in many different application fields, ranging from climate modeling, finance, reactive systems, social networks, epidemic modeling, life sciences,...
Systems driven by external noise
PC Analysis of Stochastic Differential Equations driven by Wiener noise.
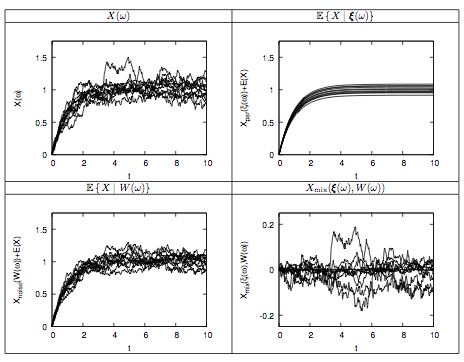 A polynomial chaos (PC) analysis with stochastic expansion coefficients is proposed for stochastic differential equations driven by additive or multiplicative Wiener noise.
It is shown that for this setting, a Galerkin formalism naturally leads to the definition of a hierarchy of stochastic differential equations governing the evolution of the PC modes.
Under the mild assumption that the Wiener and uncertain parameters can be treated as independent random variables, it is also shown that the Galerkin formalism naturally separates parametric uncertainty and stochastic forcing dependences.
This also enables us to perform an orthogonal decomposition of the process variance, and consequently identify contributions arising from the uncertainty in parameters, the stochastic forcing, and a coupled term.
Insight gained from this decomposition is illustrated in light of implementation to simplified linear and non-linear problems; the case of a stochastic bifurcation is also considered.
A polynomial chaos (PC) analysis with stochastic expansion coefficients is proposed for stochastic differential equations driven by additive or multiplicative Wiener noise.
It is shown that for this setting, a Galerkin formalism naturally leads to the definition of a hierarchy of stochastic differential equations governing the evolution of the PC modes.
Under the mild assumption that the Wiener and uncertain parameters can be treated as independent random variables, it is also shown that the Galerkin formalism naturally separates parametric uncertainty and stochastic forcing dependences.
This also enables us to perform an orthogonal decomposition of the process variance, and consequently identify contributions arising from the uncertainty in parameters, the stochastic forcing, and a coupled term.
Insight gained from this decomposition is illustrated in light of implementation to simplified linear and non-linear problems; the case of a stochastic bifurcation is also considered.
 A polynomial chaos (PC) analysis with stochastic expansion coefficients is proposed for stochastic differential equations driven by additive or multiplicative Wiener noise.
It is shown that for this setting, a Galerkin formalism naturally leads to the definition of a hierarchy of stochastic differential equations governing the evolution of the PC modes.
Under the mild assumption that the Wiener and uncertain parameters can be treated as independent random variables, it is also shown that the Galerkin formalism naturally separates parametric uncertainty and stochastic forcing dependences.
This also enables us to perform an orthogonal decomposition of the process variance, and consequently identify contributions arising from the uncertainty in parameters, the stochastic forcing, and a coupled term.
Insight gained from this decomposition is illustrated in light of implementation to simplified linear and non-linear problems; the case of a stochastic bifurcation is also considered.
A polynomial chaos (PC) analysis with stochastic expansion coefficients is proposed for stochastic differential equations driven by additive or multiplicative Wiener noise.
It is shown that for this setting, a Galerkin formalism naturally leads to the definition of a hierarchy of stochastic differential equations governing the evolution of the PC modes.
Under the mild assumption that the Wiener and uncertain parameters can be treated as independent random variables, it is also shown that the Galerkin formalism naturally separates parametric uncertainty and stochastic forcing dependences.
This also enables us to perform an orthogonal decomposition of the process variance, and consequently identify contributions arising from the uncertainty in parameters, the stochastic forcing, and a coupled term.
Insight gained from this decomposition is illustrated in light of implementation to simplified linear and non-linear problems; the case of a stochastic bifurcation is also considered.
Non-Intrusive Polynomial Chaos Expansions for Sensitivity Analysis in Stochastic Differential Equations.
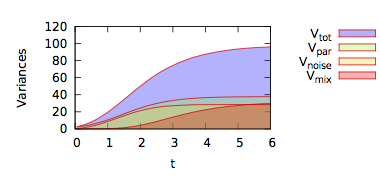 We extend the variance decomposition and sensitivity analysis in stochastic differential equations (SDEs), driven by Wiener noise and involving uncertain parameters, to non-intrusive approaches enabling its application to more complex systems hardly amenable to stochastic Galerkin projection methods.
We also discuss parallel implementations and the variance decomposition of derived quantity of interest within the framework of non-intrusive approaches.
In particular, a novel hybrid PC sampling based strategy is proposed in the case of non-smooth quantities of interest (QoIs) but smooth SDE solution.
Numerical examples are provided that illustrate the decomposition of the variance of QoIs into contributions arising from the uncertain
parameters, the inherent stochastic forcing, and joint effects.
The simulations are also used to support a brief analysis of the computational complexity of the method, providing insight on type of problems that would benefit from the present developments.
We extend the variance decomposition and sensitivity analysis in stochastic differential equations (SDEs), driven by Wiener noise and involving uncertain parameters, to non-intrusive approaches enabling its application to more complex systems hardly amenable to stochastic Galerkin projection methods.
We also discuss parallel implementations and the variance decomposition of derived quantity of interest within the framework of non-intrusive approaches.
In particular, a novel hybrid PC sampling based strategy is proposed in the case of non-smooth quantities of interest (QoIs) but smooth SDE solution.
Numerical examples are provided that illustrate the decomposition of the variance of QoIs into contributions arising from the uncertain
parameters, the inherent stochastic forcing, and joint effects.
The simulations are also used to support a brief analysis of the computational complexity of the method, providing insight on type of problems that would benefit from the present developments.
 We extend the variance decomposition and sensitivity analysis in stochastic differential equations (SDEs), driven by Wiener noise and involving uncertain parameters, to non-intrusive approaches enabling its application to more complex systems hardly amenable to stochastic Galerkin projection methods.
We also discuss parallel implementations and the variance decomposition of derived quantity of interest within the framework of non-intrusive approaches.
In particular, a novel hybrid PC sampling based strategy is proposed in the case of non-smooth quantities of interest (QoIs) but smooth SDE solution.
Numerical examples are provided that illustrate the decomposition of the variance of QoIs into contributions arising from the uncertain
parameters, the inherent stochastic forcing, and joint effects.
The simulations are also used to support a brief analysis of the computational complexity of the method, providing insight on type of problems that would benefit from the present developments.
We extend the variance decomposition and sensitivity analysis in stochastic differential equations (SDEs), driven by Wiener noise and involving uncertain parameters, to non-intrusive approaches enabling its application to more complex systems hardly amenable to stochastic Galerkin projection methods.
We also discuss parallel implementations and the variance decomposition of derived quantity of interest within the framework of non-intrusive approaches.
In particular, a novel hybrid PC sampling based strategy is proposed in the case of non-smooth quantities of interest (QoIs) but smooth SDE solution.
Numerical examples are provided that illustrate the decomposition of the variance of QoIs into contributions arising from the uncertain
parameters, the inherent stochastic forcing, and joint effects.
The simulations are also used to support a brief analysis of the computational complexity of the method, providing insight on type of problems that would benefit from the present developments.
Stochastic simulators
Variance Decomposition in Stochastic Simulators.
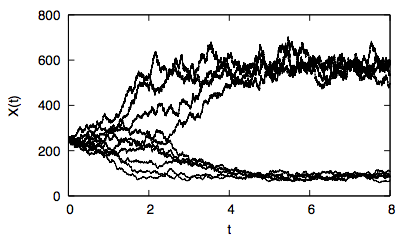 This work aims at the development of a mathematical and computational approach
that enables quantification of the inherent sources of stochasticity and of the corresponding
sensitivities in stochastic simulations of chemical reaction networks. The approach is based on reformulating the system dynamics as being generated by independent standardized Poisson processes.
This reformulation affords a straightforward identification of individual realizations for the stochastic
dynamics of each reaction channel,
and consequently a quantitative characterization of the inherent sources of stochasticity in the system. By relying on the
Sobol-Hoeffding decomposition, the reformulation enables us to perform an orthogonal
decomposition of the solution variance. Thus, by judiciously exploiting the inherent stochasticity
of the system, one is able to quantify the variance-based sensitivities associated with individual
reaction channels, as well as the importance of channel interactions. Implementation of the algorithms is
illustrated in light of simulations of simplified systems, including the birth-death,
Schlögl, and Michaelis-Menten models.
This work aims at the development of a mathematical and computational approach
that enables quantification of the inherent sources of stochasticity and of the corresponding
sensitivities in stochastic simulations of chemical reaction networks. The approach is based on reformulating the system dynamics as being generated by independent standardized Poisson processes.
This reformulation affords a straightforward identification of individual realizations for the stochastic
dynamics of each reaction channel,
and consequently a quantitative characterization of the inherent sources of stochasticity in the system. By relying on the
Sobol-Hoeffding decomposition, the reformulation enables us to perform an orthogonal
decomposition of the solution variance. Thus, by judiciously exploiting the inherent stochasticity
of the system, one is able to quantify the variance-based sensitivities associated with individual
reaction channels, as well as the importance of channel interactions. Implementation of the algorithms is
illustrated in light of simulations of simplified systems, including the birth-death,
Schlögl, and Michaelis-Menten models.
 This work aims at the development of a mathematical and computational approach
that enables quantification of the inherent sources of stochasticity and of the corresponding
sensitivities in stochastic simulations of chemical reaction networks. The approach is based on reformulating the system dynamics as being generated by independent standardized Poisson processes.
This reformulation affords a straightforward identification of individual realizations for the stochastic
dynamics of each reaction channel,
and consequently a quantitative characterization of the inherent sources of stochasticity in the system. By relying on the
Sobol-Hoeffding decomposition, the reformulation enables us to perform an orthogonal
decomposition of the solution variance. Thus, by judiciously exploiting the inherent stochasticity
of the system, one is able to quantify the variance-based sensitivities associated with individual
reaction channels, as well as the importance of channel interactions. Implementation of the algorithms is
illustrated in light of simulations of simplified systems, including the birth-death,
Schlögl, and Michaelis-Menten models.
This work aims at the development of a mathematical and computational approach
that enables quantification of the inherent sources of stochasticity and of the corresponding
sensitivities in stochastic simulations of chemical reaction networks. The approach is based on reformulating the system dynamics as being generated by independent standardized Poisson processes.
This reformulation affords a straightforward identification of individual realizations for the stochastic
dynamics of each reaction channel,
and consequently a quantitative characterization of the inherent sources of stochasticity in the system. By relying on the
Sobol-Hoeffding decomposition, the reformulation enables us to perform an orthogonal
decomposition of the solution variance. Thus, by judiciously exploiting the inherent stochasticity
of the system, one is able to quantify the variance-based sensitivities associated with individual
reaction channels, as well as the importance of channel interactions. Implementation of the algorithms is
illustrated in light of simulations of simplified systems, including the birth-death,
Schlögl, and Michaelis-Menten models.
Global Sensitivity Analysis in Stochastic Simulators of Uncertain Reaction Networks.
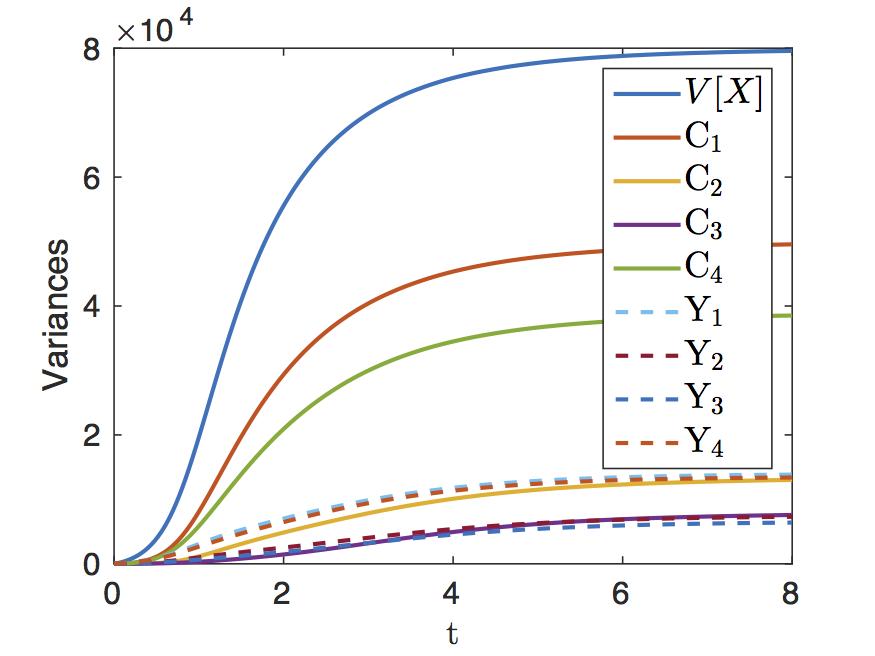 Stochastic models of chemical systems are often subjected to uncertainties in kinetic parameters in addition to the inherent random nature of their dynamics.
Uncertainty quantification in such systems is generally achieved by mean of sensitivity analyses in which one characterizes the variability with the uncertain kinetic parameters of the first statistical moments of model predictions.
In this work, we propose an original global sensitivity analysis method where the parametric and inherent variability sources are both treated through Sobol's decomposition of the variance into contributions from arbitrary subset of uncertain parameters and stochastic reaction channels. The method only assumes that the inherent and parametric sources are independent, and considers the Poisson processes in the random-time-change representation of the state dynamics as the fundamental objects governing the inherent stochasticity.
A sampling algorithm is proposed to perform the global sensitivity analysis, and to estimate the partial variances and sensitivity indices characterizing the importance of the various sources of variability and their interactions.
The birth-death and Schlögl models are used to illustrate both the implementation of the algorithm and the richness of proposed analysis method.
The output of the proposed sensitivity analysis is also contrasted with a local derivative-based sensitivity analysis method classically used for this type of systems.
Stochastic models of chemical systems are often subjected to uncertainties in kinetic parameters in addition to the inherent random nature of their dynamics.
Uncertainty quantification in such systems is generally achieved by mean of sensitivity analyses in which one characterizes the variability with the uncertain kinetic parameters of the first statistical moments of model predictions.
In this work, we propose an original global sensitivity analysis method where the parametric and inherent variability sources are both treated through Sobol's decomposition of the variance into contributions from arbitrary subset of uncertain parameters and stochastic reaction channels. The method only assumes that the inherent and parametric sources are independent, and considers the Poisson processes in the random-time-change representation of the state dynamics as the fundamental objects governing the inherent stochasticity.
A sampling algorithm is proposed to perform the global sensitivity analysis, and to estimate the partial variances and sensitivity indices characterizing the importance of the various sources of variability and their interactions.
The birth-death and Schlögl models are used to illustrate both the implementation of the algorithm and the richness of proposed analysis method.
The output of the proposed sensitivity analysis is also contrasted with a local derivative-based sensitivity analysis method classically used for this type of systems.
 Stochastic models of chemical systems are often subjected to uncertainties in kinetic parameters in addition to the inherent random nature of their dynamics.
Uncertainty quantification in such systems is generally achieved by mean of sensitivity analyses in which one characterizes the variability with the uncertain kinetic parameters of the first statistical moments of model predictions.
In this work, we propose an original global sensitivity analysis method where the parametric and inherent variability sources are both treated through Sobol's decomposition of the variance into contributions from arbitrary subset of uncertain parameters and stochastic reaction channels. The method only assumes that the inherent and parametric sources are independent, and considers the Poisson processes in the random-time-change representation of the state dynamics as the fundamental objects governing the inherent stochasticity.
A sampling algorithm is proposed to perform the global sensitivity analysis, and to estimate the partial variances and sensitivity indices characterizing the importance of the various sources of variability and their interactions.
The birth-death and Schlögl models are used to illustrate both the implementation of the algorithm and the richness of proposed analysis method.
The output of the proposed sensitivity analysis is also contrasted with a local derivative-based sensitivity analysis method classically used for this type of systems.
Stochastic models of chemical systems are often subjected to uncertainties in kinetic parameters in addition to the inherent random nature of their dynamics.
Uncertainty quantification in such systems is generally achieved by mean of sensitivity analyses in which one characterizes the variability with the uncertain kinetic parameters of the first statistical moments of model predictions.
In this work, we propose an original global sensitivity analysis method where the parametric and inherent variability sources are both treated through Sobol's decomposition of the variance into contributions from arbitrary subset of uncertain parameters and stochastic reaction channels. The method only assumes that the inherent and parametric sources are independent, and considers the Poisson processes in the random-time-change representation of the state dynamics as the fundamental objects governing the inherent stochasticity.
A sampling algorithm is proposed to perform the global sensitivity analysis, and to estimate the partial variances and sensitivity indices characterizing the importance of the various sources of variability and their interactions.
The birth-death and Schlögl models are used to illustrate both the implementation of the algorithm and the richness of proposed analysis method.
The output of the proposed sensitivity analysis is also contrasted with a local derivative-based sensitivity analysis method classically used for this type of systems.
Bayesian Inference
A large fraction of my research activities is dedicated to the use of Polynomial Chaos expansions to tackle inference problems and accelerate the resolution of Bayesian problems. These efforts can be split into methodological contributions and applicative works.
The Bayesian approach requires the prescription of a prior distribution, for the model parameters to be infered, and of the likelihood that assesses the miss-fit between the observations and the model predictions. The outcome of the analysis depending on these choices, it is important to consider general enough structures that are adapted to the actual parameters' prior, measurement noise and model error. Typically, this is achieved by introducing hyper-parameters that become part of the inference problem. These hyper-parameters call for an adaptation of the Polynomial Chaos based surrogate models, for instance to avoid having to reconstruct the whole PC model each time new hyper-parameter values are proposed. The gain can be dramatic when using Markov Chain Monte Carlo (MCMC) samplers to explore the posterior distribution of the parameters, since these chains involve typically thousands of steps. In terms of applications, we have developed and tested original methodologies on a wide range of problems through collaborative efforts. These problems include the inference, from both synthetic and real measurements, of the geometric and elastic properties of arteries and blood circulation networks, the parameters of an earthquake model in a tsunami simulator, the detection of tumors in soft tissues, the bottom friction parameters in a shallow water models.
The Bayesian approach requires the prescription of a prior distribution, for the model parameters to be infered, and of the likelihood that assesses the miss-fit between the observations and the model predictions. The outcome of the analysis depending on these choices, it is important to consider general enough structures that are adapted to the actual parameters' prior, measurement noise and model error. Typically, this is achieved by introducing hyper-parameters that become part of the inference problem. These hyper-parameters call for an adaptation of the Polynomial Chaos based surrogate models, for instance to avoid having to reconstruct the whole PC model each time new hyper-parameter values are proposed. The gain can be dramatic when using Markov Chain Monte Carlo (MCMC) samplers to explore the posterior distribution of the parameters, since these chains involve typically thousands of steps. In terms of applications, we have developed and tested original methodologies on a wide range of problems through collaborative efforts. These problems include the inference, from both synthetic and real measurements, of the geometric and elastic properties of arteries and blood circulation networks, the parameters of an earthquake model in a tsunami simulator, the detection of tumors in soft tissues, the bottom friction parameters in a shallow water models.
Surrogate modeling for Bayesian Inference
Coordinate Transformation and Polynomial Chaos for the Bayesian Inference of a Gaussian Process with Parametrized Prior Covariance Function.
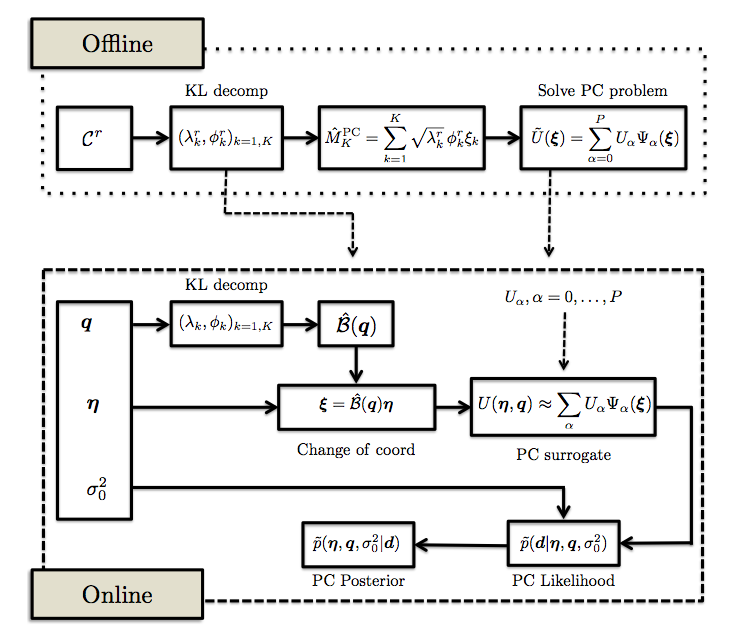 This work addresses model dimensionality reduction for Bayesian inference based on prior Gaussian fields with uncertainty in the covariance function hyper-parameters.
The dimensionality reduction is traditionally achieved using the Karhunen-Loeve expansion of a prior Gaussian process assuming covariance function with fixed hyper-parameters, despite the fact that these are uncertain in nature.
The posterior distribution of the Karhunen-Loeve coordinates is then inferred using available observations.
The resulting inferred field is therefore dependent on the assumed hyper-parameters.
Here, we seek to efficiently estimate both the field and covariance hyper-parameters using
Bayesian inference. To this end, a generalized Karhunen-Loeve expansion is derived using a coordinate transformation to account for the dependence with respect to the covariance hyper-parameters.
Polynomial Chaos expansions are employed for the acceleration of the Bayesian inference using similar coordinate transformations,
enabling us to avoid expanding explicitly the solution dependence on the uncertain hyper-parameters.
We demonstrate the feasibility of the proposed method on a transient diffusion equation
by inferring spatially-varying log-diffusivity fields from noisy data. The inferred profiles
were found closer to the true profiles when including the hyper-parameters' uncertainty
in the inference formulation.
This work addresses model dimensionality reduction for Bayesian inference based on prior Gaussian fields with uncertainty in the covariance function hyper-parameters.
The dimensionality reduction is traditionally achieved using the Karhunen-Loeve expansion of a prior Gaussian process assuming covariance function with fixed hyper-parameters, despite the fact that these are uncertain in nature.
The posterior distribution of the Karhunen-Loeve coordinates is then inferred using available observations.
The resulting inferred field is therefore dependent on the assumed hyper-parameters.
Here, we seek to efficiently estimate both the field and covariance hyper-parameters using
Bayesian inference. To this end, a generalized Karhunen-Loeve expansion is derived using a coordinate transformation to account for the dependence with respect to the covariance hyper-parameters.
Polynomial Chaos expansions are employed for the acceleration of the Bayesian inference using similar coordinate transformations,
enabling us to avoid expanding explicitly the solution dependence on the uncertain hyper-parameters.
We demonstrate the feasibility of the proposed method on a transient diffusion equation
by inferring spatially-varying log-diffusivity fields from noisy data. The inferred profiles
were found closer to the true profiles when including the hyper-parameters' uncertainty
in the inference formulation.
 This work addresses model dimensionality reduction for Bayesian inference based on prior Gaussian fields with uncertainty in the covariance function hyper-parameters.
The dimensionality reduction is traditionally achieved using the Karhunen-Loeve expansion of a prior Gaussian process assuming covariance function with fixed hyper-parameters, despite the fact that these are uncertain in nature.
The posterior distribution of the Karhunen-Loeve coordinates is then inferred using available observations.
The resulting inferred field is therefore dependent on the assumed hyper-parameters.
Here, we seek to efficiently estimate both the field and covariance hyper-parameters using
Bayesian inference. To this end, a generalized Karhunen-Loeve expansion is derived using a coordinate transformation to account for the dependence with respect to the covariance hyper-parameters.
Polynomial Chaos expansions are employed for the acceleration of the Bayesian inference using similar coordinate transformations,
enabling us to avoid expanding explicitly the solution dependence on the uncertain hyper-parameters.
We demonstrate the feasibility of the proposed method on a transient diffusion equation
by inferring spatially-varying log-diffusivity fields from noisy data. The inferred profiles
were found closer to the true profiles when including the hyper-parameters' uncertainty
in the inference formulation.
This work addresses model dimensionality reduction for Bayesian inference based on prior Gaussian fields with uncertainty in the covariance function hyper-parameters.
The dimensionality reduction is traditionally achieved using the Karhunen-Loeve expansion of a prior Gaussian process assuming covariance function with fixed hyper-parameters, despite the fact that these are uncertain in nature.
The posterior distribution of the Karhunen-Loeve coordinates is then inferred using available observations.
The resulting inferred field is therefore dependent on the assumed hyper-parameters.
Here, we seek to efficiently estimate both the field and covariance hyper-parameters using
Bayesian inference. To this end, a generalized Karhunen-Loeve expansion is derived using a coordinate transformation to account for the dependence with respect to the covariance hyper-parameters.
Polynomial Chaos expansions are employed for the acceleration of the Bayesian inference using similar coordinate transformations,
enabling us to avoid expanding explicitly the solution dependence on the uncertain hyper-parameters.
We demonstrate the feasibility of the proposed method on a transient diffusion equation
by inferring spatially-varying log-diffusivity fields from noisy data. The inferred profiles
were found closer to the true profiles when including the hyper-parameters' uncertainty
in the inference formulation.
Multi-Model Polynomial Chaos Surrogate Dictionary for Bayesian Inference in Elasticity Problems.
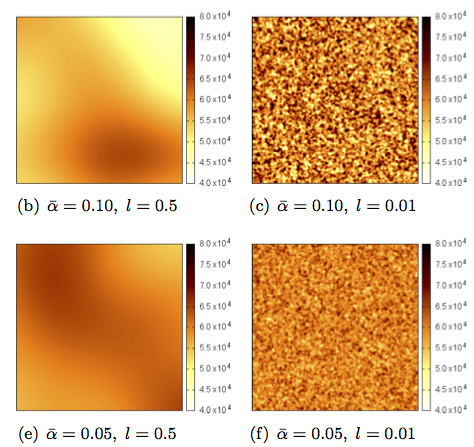 A method is presented for inferring the presence of an inclusion inside a domain; the proposed approach is suitable to be used in a diagnostic device with low computational power. Specifically, we use the Bayesian framework for the inference of stiff inclusions embedded in a soft matrix, mimicking tumors in soft tissues. We rely on a Polynomial Chaos (PC) surrogate to accelerate the inference process. The PC surrogate predicts the dependence of the displacements field with the random elastic moduli of the materials, and are computed by means of the Stochastic Galerkin (SG) projection method. Moreover, the inclusion’s geometry is assumed to be unknown, and this is addressed by using a dictionary consisting of several geometrical models with different configurations. A model selection approach based on the evidence provided by the data (Bayes factors) is used to discriminate among the different geometrical models and select the most suitable one. The idea of using a dictionary of precomputed geometrical models helps to maintain the computational cost of the inference process very low, as most of the computational burden is carried out off-line for the resolution of the SG problems. Numerical tests are used to validate the methodology, assess its performance, and analyze the robustness to model errors.
A method is presented for inferring the presence of an inclusion inside a domain; the proposed approach is suitable to be used in a diagnostic device with low computational power. Specifically, we use the Bayesian framework for the inference of stiff inclusions embedded in a soft matrix, mimicking tumors in soft tissues. We rely on a Polynomial Chaos (PC) surrogate to accelerate the inference process. The PC surrogate predicts the dependence of the displacements field with the random elastic moduli of the materials, and are computed by means of the Stochastic Galerkin (SG) projection method. Moreover, the inclusion’s geometry is assumed to be unknown, and this is addressed by using a dictionary consisting of several geometrical models with different configurations. A model selection approach based on the evidence provided by the data (Bayes factors) is used to discriminate among the different geometrical models and select the most suitable one. The idea of using a dictionary of precomputed geometrical models helps to maintain the computational cost of the inference process very low, as most of the computational burden is carried out off-line for the resolution of the SG problems. Numerical tests are used to validate the methodology, assess its performance, and analyze the robustness to model errors.
 A method is presented for inferring the presence of an inclusion inside a domain; the proposed approach is suitable to be used in a diagnostic device with low computational power. Specifically, we use the Bayesian framework for the inference of stiff inclusions embedded in a soft matrix, mimicking tumors in soft tissues. We rely on a Polynomial Chaos (PC) surrogate to accelerate the inference process. The PC surrogate predicts the dependence of the displacements field with the random elastic moduli of the materials, and are computed by means of the Stochastic Galerkin (SG) projection method. Moreover, the inclusion’s geometry is assumed to be unknown, and this is addressed by using a dictionary consisting of several geometrical models with different configurations. A model selection approach based on the evidence provided by the data (Bayes factors) is used to discriminate among the different geometrical models and select the most suitable one. The idea of using a dictionary of precomputed geometrical models helps to maintain the computational cost of the inference process very low, as most of the computational burden is carried out off-line for the resolution of the SG problems. Numerical tests are used to validate the methodology, assess its performance, and analyze the robustness to model errors.
A method is presented for inferring the presence of an inclusion inside a domain; the proposed approach is suitable to be used in a diagnostic device with low computational power. Specifically, we use the Bayesian framework for the inference of stiff inclusions embedded in a soft matrix, mimicking tumors in soft tissues. We rely on a Polynomial Chaos (PC) surrogate to accelerate the inference process. The PC surrogate predicts the dependence of the displacements field with the random elastic moduli of the materials, and are computed by means of the Stochastic Galerkin (SG) projection method. Moreover, the inclusion’s geometry is assumed to be unknown, and this is addressed by using a dictionary consisting of several geometrical models with different configurations. A model selection approach based on the evidence provided by the data (Bayes factors) is used to discriminate among the different geometrical models and select the most suitable one. The idea of using a dictionary of precomputed geometrical models helps to maintain the computational cost of the inference process very low, as most of the computational burden is carried out off-line for the resolution of the SG problems. Numerical tests are used to validate the methodology, assess its performance, and analyze the robustness to model errors.
Application of Bayesian Inference
Simultaneous identification of elastic properties, thickness, and diameter of arteries excited with ultrasound radiation force.
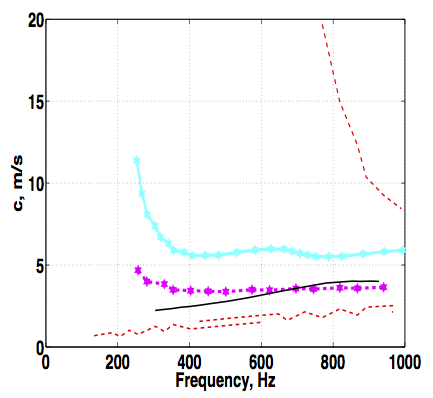 The elastic and geometric properties of arteries have been long recognized as important predictors of cardiovascular disease. This work presents a robust technique for the noninvasive characterization of anisotropic elastic properties as well as thickness and diameter in arterial vessels. In our approach, guided waves are excited along arteries using the radiation force of ultrasound. Group velocity is used as the quantity of interest to reconstruct elastic and geometric features of the vessels. One of the main contributions of this work is a systematic approach based on sparse-grid collocation interpolation to construct surrogate models of arteries. These surrogate models are in turn used with direct-search optimization techniques to produce fast and accurate estimates of elastic properties, diameter, and thickness. One of the attractive features of the proposed approach is that once a surrogate model is built, it can be used for near real-time identification across many different types of arteries. We demonstrate the feasibility of the method using simulated and in vitro laboratory experiments on a silicon rubber tube and a porcine carotid artery. Our results show that using our proposed method, we can reliably identify the longitudinal modulus, thickness, and diameter of arteries. The circumferential modulus was found to have little influence in the group velocity, which renders the former quantity unidentifiable using the current experimental setting. Future work will consider the measurement of circumferential waves with the objective of improving the identifiability of the circumferential modulus.
The elastic and geometric properties of arteries have been long recognized as important predictors of cardiovascular disease. This work presents a robust technique for the noninvasive characterization of anisotropic elastic properties as well as thickness and diameter in arterial vessels. In our approach, guided waves are excited along arteries using the radiation force of ultrasound. Group velocity is used as the quantity of interest to reconstruct elastic and geometric features of the vessels. One of the main contributions of this work is a systematic approach based on sparse-grid collocation interpolation to construct surrogate models of arteries. These surrogate models are in turn used with direct-search optimization techniques to produce fast and accurate estimates of elastic properties, diameter, and thickness. One of the attractive features of the proposed approach is that once a surrogate model is built, it can be used for near real-time identification across many different types of arteries. We demonstrate the feasibility of the method using simulated and in vitro laboratory experiments on a silicon rubber tube and a porcine carotid artery. Our results show that using our proposed method, we can reliably identify the longitudinal modulus, thickness, and diameter of arteries. The circumferential modulus was found to have little influence in the group velocity, which renders the former quantity unidentifiable using the current experimental setting. Future work will consider the measurement of circumferential waves with the objective of improving the identifiability of the circumferential modulus.
 The elastic and geometric properties of arteries have been long recognized as important predictors of cardiovascular disease. This work presents a robust technique for the noninvasive characterization of anisotropic elastic properties as well as thickness and diameter in arterial vessels. In our approach, guided waves are excited along arteries using the radiation force of ultrasound. Group velocity is used as the quantity of interest to reconstruct elastic and geometric features of the vessels. One of the main contributions of this work is a systematic approach based on sparse-grid collocation interpolation to construct surrogate models of arteries. These surrogate models are in turn used with direct-search optimization techniques to produce fast and accurate estimates of elastic properties, diameter, and thickness. One of the attractive features of the proposed approach is that once a surrogate model is built, it can be used for near real-time identification across many different types of arteries. We demonstrate the feasibility of the method using simulated and in vitro laboratory experiments on a silicon rubber tube and a porcine carotid artery. Our results show that using our proposed method, we can reliably identify the longitudinal modulus, thickness, and diameter of arteries. The circumferential modulus was found to have little influence in the group velocity, which renders the former quantity unidentifiable using the current experimental setting. Future work will consider the measurement of circumferential waves with the objective of improving the identifiability of the circumferential modulus.
The elastic and geometric properties of arteries have been long recognized as important predictors of cardiovascular disease. This work presents a robust technique for the noninvasive characterization of anisotropic elastic properties as well as thickness and diameter in arterial vessels. In our approach, guided waves are excited along arteries using the radiation force of ultrasound. Group velocity is used as the quantity of interest to reconstruct elastic and geometric features of the vessels. One of the main contributions of this work is a systematic approach based on sparse-grid collocation interpolation to construct surrogate models of arteries. These surrogate models are in turn used with direct-search optimization techniques to produce fast and accurate estimates of elastic properties, diameter, and thickness. One of the attractive features of the proposed approach is that once a surrogate model is built, it can be used for near real-time identification across many different types of arteries. We demonstrate the feasibility of the method using simulated and in vitro laboratory experiments on a silicon rubber tube and a porcine carotid artery. Our results show that using our proposed method, we can reliably identify the longitudinal modulus, thickness, and diameter of arteries. The circumferential modulus was found to have little influence in the group velocity, which renders the former quantity unidentifiable using the current experimental setting. Future work will consider the measurement of circumferential waves with the objective of improving the identifiability of the circumferential modulus.
Bayesian inference of earthquake parameters from buoy data using Polynomial Chaos based surrogate.
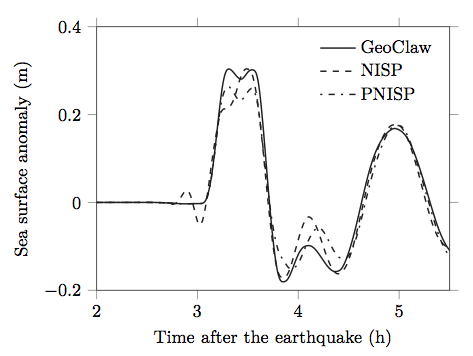 This work addresses the estimation of the parameters of an earthquake model through the generated tsunami, with an application to the Chile 2010 event. We are particularly interested in the Bayesian inference of the location, the orientation and the slip of the Okada model of the earthquake. The computational tsunami model is based on the GeoClaw software, while the data are provided by a single DART buoy. We propose in this paper a methodology based on polynomial chaos expansion in order to construct a surrogate model of the wave height at the buoy location. A correlated noise model is first proposed in order to represent the discrepancy between the computational model and the data. This step is necessary, as a classical independent Gaussian noise is shown to be unsuitable for modeling the error, and to prevent convergence of the Markov-Chain Monte-Carlo sampler. Second, the polynomial chaos model is subsequently improved to handle the variability of the arrival time of the wave, using a preconditioned non-intrusive spectral method. Finally, the construction of a reduced model dedicated to Bayesian inference is proposed. Numerical results are presented and discussed.
This work addresses the estimation of the parameters of an earthquake model through the generated tsunami, with an application to the Chile 2010 event. We are particularly interested in the Bayesian inference of the location, the orientation and the slip of the Okada model of the earthquake. The computational tsunami model is based on the GeoClaw software, while the data are provided by a single DART buoy. We propose in this paper a methodology based on polynomial chaos expansion in order to construct a surrogate model of the wave height at the buoy location. A correlated noise model is first proposed in order to represent the discrepancy between the computational model and the data. This step is necessary, as a classical independent Gaussian noise is shown to be unsuitable for modeling the error, and to prevent convergence of the Markov-Chain Monte-Carlo sampler. Second, the polynomial chaos model is subsequently improved to handle the variability of the arrival time of the wave, using a preconditioned non-intrusive spectral method. Finally, the construction of a reduced model dedicated to Bayesian inference is proposed. Numerical results are presented and discussed.
 This work addresses the estimation of the parameters of an earthquake model through the generated tsunami, with an application to the Chile 2010 event. We are particularly interested in the Bayesian inference of the location, the orientation and the slip of the Okada model of the earthquake. The computational tsunami model is based on the GeoClaw software, while the data are provided by a single DART buoy. We propose in this paper a methodology based on polynomial chaos expansion in order to construct a surrogate model of the wave height at the buoy location. A correlated noise model is first proposed in order to represent the discrepancy between the computational model and the data. This step is necessary, as a classical independent Gaussian noise is shown to be unsuitable for modeling the error, and to prevent convergence of the Markov-Chain Monte-Carlo sampler. Second, the polynomial chaos model is subsequently improved to handle the variability of the arrival time of the wave, using a preconditioned non-intrusive spectral method. Finally, the construction of a reduced model dedicated to Bayesian inference is proposed. Numerical results are presented and discussed.
This work addresses the estimation of the parameters of an earthquake model through the generated tsunami, with an application to the Chile 2010 event. We are particularly interested in the Bayesian inference of the location, the orientation and the slip of the Okada model of the earthquake. The computational tsunami model is based on the GeoClaw software, while the data are provided by a single DART buoy. We propose in this paper a methodology based on polynomial chaos expansion in order to construct a surrogate model of the wave height at the buoy location. A correlated noise model is first proposed in order to represent the discrepancy between the computational model and the data. This step is necessary, as a classical independent Gaussian noise is shown to be unsuitable for modeling the error, and to prevent convergence of the Markov-Chain Monte-Carlo sampler. Second, the polynomial chaos model is subsequently improved to handle the variability of the arrival time of the wave, using a preconditioned non-intrusive spectral method. Finally, the construction of a reduced model dedicated to Bayesian inference is proposed. Numerical results are presented and discussed.
Optimization under Uncertainty
In addition to the acceleration of Bayesian inference problems, we also apply our expertise on surrogate models to several optimization problems, more precisely in the domain of optimization under uncertainty.
So far, our contributions have consisted in the deployment of sampling strategies to investigate the robustness of (optimal) path planing solutions for autonomous underwater vehicles evolving in uncertain flows and the statistical characterization and robustness analysis of the optimal trimming of a sail in a experimental and numerical wind-tunnel.
Path Planning in Uncertain Flow Fields using Ensemble Method.
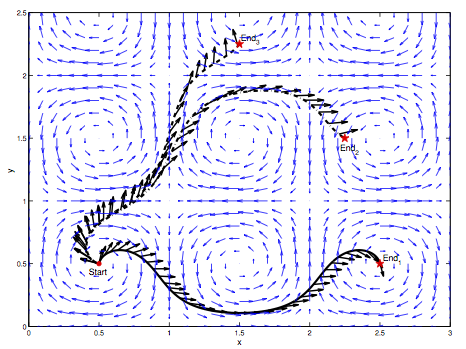 An ensemble-based approach is developed to conduct optimal path planning in unsteady ocean currents under uncertainty.
We focus our attention on two-dimensional steady and unsteady uncertain flows, and adopt a sampling methodology that is well suited to operational forecasts, where an ensemble of deterministic predictions is used to model and quantify uncertainty.
In an operational setting, much about dynamics, topography and forcing of the ocean environment is uncertain.
To address this uncertainty, the flow field is parametrized using a finite number of independent canonical random variables with known densities, and the ensemble is generated by sampling these variables.
For each of the resulting realizations of the uncertain current field, we predict the path that minimizes the travel time by solving a boundary value problem (BVP), based on the Pontryagin maximum principle.
A family of backward-in-time trajectories starting at the end position is used to generate suitable initial values for the BVP solver.
This allows us to examine and analyze the performance of the sampling strategy, and to develop insight into extensions dealing with general circulation ocean models.
In particular, the ensemble method enables us to perform a statistical analysis of travel times, and consequently develop a path planning approach that accounts for these statistics.
The proposed methodology is tested for a number of scenarios. We first validate our algorithms by reproducing simple canonical solutions, and then demonstrate our approach in more complex flow fields, including idealized, steady and unsteady double-gyre flows.
An ensemble-based approach is developed to conduct optimal path planning in unsteady ocean currents under uncertainty.
We focus our attention on two-dimensional steady and unsteady uncertain flows, and adopt a sampling methodology that is well suited to operational forecasts, where an ensemble of deterministic predictions is used to model and quantify uncertainty.
In an operational setting, much about dynamics, topography and forcing of the ocean environment is uncertain.
To address this uncertainty, the flow field is parametrized using a finite number of independent canonical random variables with known densities, and the ensemble is generated by sampling these variables.
For each of the resulting realizations of the uncertain current field, we predict the path that minimizes the travel time by solving a boundary value problem (BVP), based on the Pontryagin maximum principle.
A family of backward-in-time trajectories starting at the end position is used to generate suitable initial values for the BVP solver.
This allows us to examine and analyze the performance of the sampling strategy, and to develop insight into extensions dealing with general circulation ocean models.
In particular, the ensemble method enables us to perform a statistical analysis of travel times, and consequently develop a path planning approach that accounts for these statistics.
The proposed methodology is tested for a number of scenarios. We first validate our algorithms by reproducing simple canonical solutions, and then demonstrate our approach in more complex flow fields, including idealized, steady and unsteady double-gyre flows.
 An ensemble-based approach is developed to conduct optimal path planning in unsteady ocean currents under uncertainty.
We focus our attention on two-dimensional steady and unsteady uncertain flows, and adopt a sampling methodology that is well suited to operational forecasts, where an ensemble of deterministic predictions is used to model and quantify uncertainty.
In an operational setting, much about dynamics, topography and forcing of the ocean environment is uncertain.
To address this uncertainty, the flow field is parametrized using a finite number of independent canonical random variables with known densities, and the ensemble is generated by sampling these variables.
For each of the resulting realizations of the uncertain current field, we predict the path that minimizes the travel time by solving a boundary value problem (BVP), based on the Pontryagin maximum principle.
A family of backward-in-time trajectories starting at the end position is used to generate suitable initial values for the BVP solver.
This allows us to examine and analyze the performance of the sampling strategy, and to develop insight into extensions dealing with general circulation ocean models.
In particular, the ensemble method enables us to perform a statistical analysis of travel times, and consequently develop a path planning approach that accounts for these statistics.
The proposed methodology is tested for a number of scenarios. We first validate our algorithms by reproducing simple canonical solutions, and then demonstrate our approach in more complex flow fields, including idealized, steady and unsteady double-gyre flows.
An ensemble-based approach is developed to conduct optimal path planning in unsteady ocean currents under uncertainty.
We focus our attention on two-dimensional steady and unsteady uncertain flows, and adopt a sampling methodology that is well suited to operational forecasts, where an ensemble of deterministic predictions is used to model and quantify uncertainty.
In an operational setting, much about dynamics, topography and forcing of the ocean environment is uncertain.
To address this uncertainty, the flow field is parametrized using a finite number of independent canonical random variables with known densities, and the ensemble is generated by sampling these variables.
For each of the resulting realizations of the uncertain current field, we predict the path that minimizes the travel time by solving a boundary value problem (BVP), based on the Pontryagin maximum principle.
A family of backward-in-time trajectories starting at the end position is used to generate suitable initial values for the BVP solver.
This allows us to examine and analyze the performance of the sampling strategy, and to develop insight into extensions dealing with general circulation ocean models.
In particular, the ensemble method enables us to perform a statistical analysis of travel times, and consequently develop a path planning approach that accounts for these statistics.
The proposed methodology is tested for a number of scenarios. We first validate our algorithms by reproducing simple canonical solutions, and then demonstrate our approach in more complex flow fields, including idealized, steady and unsteady double-gyre flows.
Efficient Optimization Procedure in Non-Linear Fluid-Structure Interaction Problem: Application to Mainsail Trimming in Upwind Conditions.
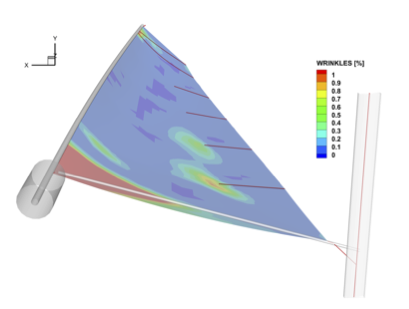 This work investigates the use of Gaussian Processes to solve sail trimming optimization problems.
The Gaussian process, used to model the dependence of the performance with the trimming parameters, is constructed from a limited number of performance estimations at carefully selected trimming points, potentially enabling the optimization of complex sail systems with multiple trimming parameters.
The proposed approach is tested on a two-parameter trimming for a scaled IMOCA mainsail in upwind sailing conditions.
We focus on the robustness of the proposed approach and study especially the sensitivity of the results to noise and model error in the point estimations of the performance.
In particular, we contrast the optimization performed on a real physical model set in a wind tunnel with a fully non-linear numerical fluid structure interaction model of the same experiments.
For this problem with a limited number of trimming parameters, the numerical optimization was affordable and found to require a comparable amount of performance estimation as for the experimental case.
The results reveal a satisfactory agreement for the numerical and experimental optimal trimming parameters, considering the inherent sources of errors and uncertainties in both numerical and experimental approaches.
Sensitivity analyses have been eventually performed in the numerical optimization problem to determine the dominant source of uncertainties and characterize the robustness of the optima.
This work investigates the use of Gaussian Processes to solve sail trimming optimization problems.
The Gaussian process, used to model the dependence of the performance with the trimming parameters, is constructed from a limited number of performance estimations at carefully selected trimming points, potentially enabling the optimization of complex sail systems with multiple trimming parameters.
The proposed approach is tested on a two-parameter trimming for a scaled IMOCA mainsail in upwind sailing conditions.
We focus on the robustness of the proposed approach and study especially the sensitivity of the results to noise and model error in the point estimations of the performance.
In particular, we contrast the optimization performed on a real physical model set in a wind tunnel with a fully non-linear numerical fluid structure interaction model of the same experiments.
For this problem with a limited number of trimming parameters, the numerical optimization was affordable and found to require a comparable amount of performance estimation as for the experimental case.
The results reveal a satisfactory agreement for the numerical and experimental optimal trimming parameters, considering the inherent sources of errors and uncertainties in both numerical and experimental approaches.
Sensitivity analyses have been eventually performed in the numerical optimization problem to determine the dominant source of uncertainties and characterize the robustness of the optima.
 This work investigates the use of Gaussian Processes to solve sail trimming optimization problems.
The Gaussian process, used to model the dependence of the performance with the trimming parameters, is constructed from a limited number of performance estimations at carefully selected trimming points, potentially enabling the optimization of complex sail systems with multiple trimming parameters.
The proposed approach is tested on a two-parameter trimming for a scaled IMOCA mainsail in upwind sailing conditions.
We focus on the robustness of the proposed approach and study especially the sensitivity of the results to noise and model error in the point estimations of the performance.
In particular, we contrast the optimization performed on a real physical model set in a wind tunnel with a fully non-linear numerical fluid structure interaction model of the same experiments.
For this problem with a limited number of trimming parameters, the numerical optimization was affordable and found to require a comparable amount of performance estimation as for the experimental case.
The results reveal a satisfactory agreement for the numerical and experimental optimal trimming parameters, considering the inherent sources of errors and uncertainties in both numerical and experimental approaches.
Sensitivity analyses have been eventually performed in the numerical optimization problem to determine the dominant source of uncertainties and characterize the robustness of the optima.
This work investigates the use of Gaussian Processes to solve sail trimming optimization problems.
The Gaussian process, used to model the dependence of the performance with the trimming parameters, is constructed from a limited number of performance estimations at carefully selected trimming points, potentially enabling the optimization of complex sail systems with multiple trimming parameters.
The proposed approach is tested on a two-parameter trimming for a scaled IMOCA mainsail in upwind sailing conditions.
We focus on the robustness of the proposed approach and study especially the sensitivity of the results to noise and model error in the point estimations of the performance.
In particular, we contrast the optimization performed on a real physical model set in a wind tunnel with a fully non-linear numerical fluid structure interaction model of the same experiments.
For this problem with a limited number of trimming parameters, the numerical optimization was affordable and found to require a comparable amount of performance estimation as for the experimental case.
The results reveal a satisfactory agreement for the numerical and experimental optimal trimming parameters, considering the inherent sources of errors and uncertainties in both numerical and experimental approaches.
Sensitivity analyses have been eventually performed in the numerical optimization problem to determine the dominant source of uncertainties and characterize the robustness of the optima.
Scientific Computing & HPC
The constant development of modern computational infrastructures offers both opportunities and challenges to advance simulation capabilities. For instance, progresses in computational power allow to tackle more complete and detailed modeling of ever more realistic systems within reasonable computational times. These promises are particularly appealing in the context of uncertainty management that usually requires many more simulations to be be performed.
On the other hand, exploiting of the potential of new massively parallel computers calls for a constant effort to adapt codes and algorithms, in order to make them suitable to the evolving architectures.
On the other hand, exploiting of the potential of new massively parallel computers calls for a constant effort to adapt codes and algorithms, in order to make them suitable to the evolving architectures.
Resilient Computing
The move toward extreme-scale computing platforms challenges scientific simulations in many ways.
Given the recent tendencies in computer architecture development, one needs to reformulate legacy codes in order to cope with large amounts of communication, system faults and requirements of low-memory usage per core.
In this project, we focus on the development of resilient solvers for elliptic equations. Concerning soft-faults (Soft-faults are silent faults that go undetected, without halting the computation), we developed a Domain Decomposition method with a new sampling strategy to reconstruct the global boundary-to-boundary map from multiple parallel local simulations. The resiliency is ensured during the reconstruction stage which is performed on sand-boxed servers. The original algorithm was improved and extended to elliptic equations with stochastic coefficients. In the case of linear elliptic equations, the overhead of the resilient algorithm was significantly reduced by rejecting corrupted samples, based on a verification of the local solutions using cheaply computable theoretical bounds, specifically developed on purpose.
The algorithms were implemented in a dedicated computational framework simulating massively parallel machines; various faults were considered, including system faults (disable network parts, failure of computational cores and clients,...), to prove the resilience and scalability of the approach.
Fault Resilient Domain Decomposition Preconditioner for PDEs.
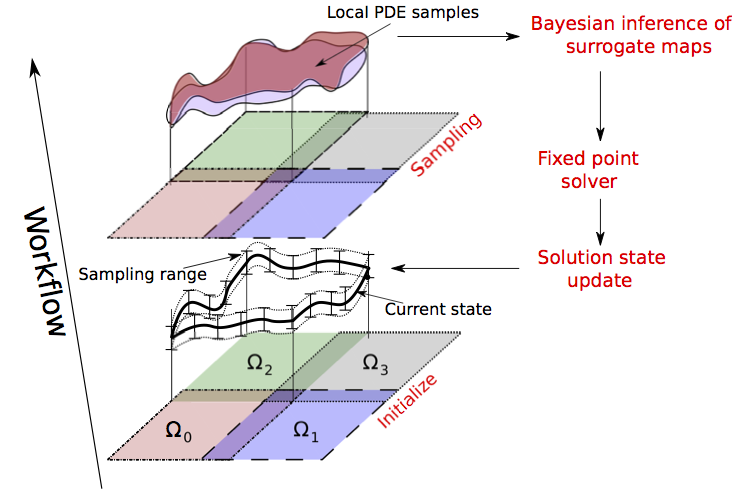 In this work, we develop a novel framework for solving partial differential equations (PDEs) via domain decomposition that reformulates the solution as a state-of-knowledge with a probabilistic interpretation.
Such reformulation allows resiliency with respect to potential faults without having to apply fault detection, avoids unnecessary communication and is generally well-suited for rigorous uncertainty quantification studies that target improvements of predictive fidelity of scientific models.
We demonstrate our algorithm for one-dimensional PDE examples where artificial faults have been implemented as bit-flips in the binary representation of subdomain solutions.
In this work, we develop a novel framework for solving partial differential equations (PDEs) via domain decomposition that reformulates the solution as a state-of-knowledge with a probabilistic interpretation.
Such reformulation allows resiliency with respect to potential faults without having to apply fault detection, avoids unnecessary communication and is generally well-suited for rigorous uncertainty quantification studies that target improvements of predictive fidelity of scientific models.
We demonstrate our algorithm for one-dimensional PDE examples where artificial faults have been implemented as bit-flips in the binary representation of subdomain solutions.
Bound Verification for Soft-Fault Resilience.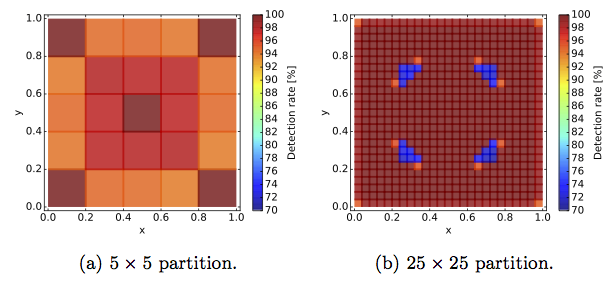 A priori bounds are derived for the discrete solution of second-order, elliptic partial differential equations (PDEs).
The bounds have two contributions. On the one hand, the influence of boundary conditions is taken into account through a discrete maximum principle. On the other hand, the contribution of the source field is evaluated in a fashion similar to that used in the treatment of the continuous a priori operators.
Closed form expressions are in particular obtained for the case of a conservative, second-order finite difference approximation of the diffusion equation with variable scalar diffusivity.
The bounds are then incorporated into a resilient domain decomposition framework, namely to verify the admissibility of local PDE solutions.
The computations demonstrate that the bounds are able to detect most of system faults, and thus considerably enhance the resilience of the solver, as well as its overall performance.
A priori bounds are derived for the discrete solution of second-order, elliptic partial differential equations (PDEs).
The bounds have two contributions. On the one hand, the influence of boundary conditions is taken into account through a discrete maximum principle. On the other hand, the contribution of the source field is evaluated in a fashion similar to that used in the treatment of the continuous a priori operators.
Closed form expressions are in particular obtained for the case of a conservative, second-order finite difference approximation of the diffusion equation with variable scalar diffusivity.
The bounds are then incorporated into a resilient domain decomposition framework, namely to verify the admissibility of local PDE solutions.
The computations demonstrate that the bounds are able to detect most of system faults, and thus considerably enhance the resilience of the solver, as well as its overall performance.
A Resilient Domain Decomposition Polynomial Chaos Solver for Uncertain Elliptic PDEs.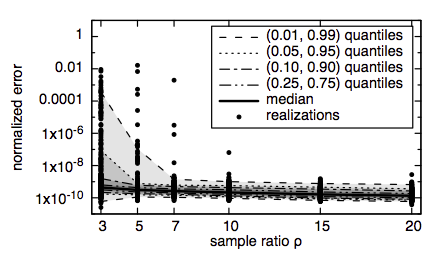 The resilient method is extended for the solution of uncertain elliptic PDEs on extreme scale platforms.
The method is based on a hybrid domain decomposition, polynomial chaos (PC) framework that is designed to address soft faults.
Specifically, parallel and independent solves of multiple deterministic local problems are used to define PC representations of local Dirichlet boundary-to-boundary maps that are used to reconstruct the global solution.
A LAD-lasso type regression is developed for this purpose.
The performance of the resulting algorithm is tested on an elliptic equation with an uncertain diffusivity field.
Different test cases are considered in order to analyze the impacts of correlation structure of the uncertain diffusivity field, the stochastic resolution, as well as the probability of soft faults.
In particular, the computations demonstrate that, provided sufficiently many samples are generated, the method effectively overcomes the occurrence of soft faults.
The resilient method is extended for the solution of uncertain elliptic PDEs on extreme scale platforms.
The method is based on a hybrid domain decomposition, polynomial chaos (PC) framework that is designed to address soft faults.
Specifically, parallel and independent solves of multiple deterministic local problems are used to define PC representations of local Dirichlet boundary-to-boundary maps that are used to reconstruct the global solution.
A LAD-lasso type regression is developed for this purpose.
The performance of the resulting algorithm is tested on an elliptic equation with an uncertain diffusivity field.
Different test cases are considered in order to analyze the impacts of correlation structure of the uncertain diffusivity field, the stochastic resolution, as well as the probability of soft faults.
In particular, the computations demonstrate that, provided sufficiently many samples are generated, the method effectively overcomes the occurrence of soft faults.
Exascale Implementation.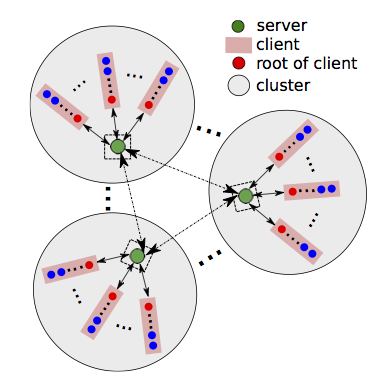 The resilient algorithms have been implementated on a server-client model where all state information is held by the servers, while clients are designed solely as computational units.
Scalability tests run up to ~51 K cores show an efficiency greater than 90%.
We use a 2D elliptic PDE and a fault model based on random single bit-flip to demonstrate the resilience
of the application to synthetically injected SDC.
We discuss two fault scenarios: one based on the corruption of all data of a target task,
and the other involving the corruption of a single data point.
We show that for our application, given the test problem considered, the overhead
incurred to overcome the presence of SDC is minimal (less than 7%).
We then discuss potential savings in energy consumption via dynamics voltage/frequency scaling,
and its interplay with fault-rates, and application overhead.
The resilient algorithms have been implementated on a server-client model where all state information is held by the servers, while clients are designed solely as computational units.
Scalability tests run up to ~51 K cores show an efficiency greater than 90%.
We use a 2D elliptic PDE and a fault model based on random single bit-flip to demonstrate the resilience
of the application to synthetically injected SDC.
We discuss two fault scenarios: one based on the corruption of all data of a target task,
and the other involving the corruption of a single data point.
We show that for our application, given the test problem considered, the overhead
incurred to overcome the presence of SDC is minimal (less than 7%).
We then discuss potential savings in energy consumption via dynamics voltage/frequency scaling,
and its interplay with fault-rates, and application overhead.
 In this work, we develop a novel framework for solving partial differential equations (PDEs) via domain decomposition that reformulates the solution as a state-of-knowledge with a probabilistic interpretation.
Such reformulation allows resiliency with respect to potential faults without having to apply fault detection, avoids unnecessary communication and is generally well-suited for rigorous uncertainty quantification studies that target improvements of predictive fidelity of scientific models.
We demonstrate our algorithm for one-dimensional PDE examples where artificial faults have been implemented as bit-flips in the binary representation of subdomain solutions.
In this work, we develop a novel framework for solving partial differential equations (PDEs) via domain decomposition that reformulates the solution as a state-of-knowledge with a probabilistic interpretation.
Such reformulation allows resiliency with respect to potential faults without having to apply fault detection, avoids unnecessary communication and is generally well-suited for rigorous uncertainty quantification studies that target improvements of predictive fidelity of scientific models.
We demonstrate our algorithm for one-dimensional PDE examples where artificial faults have been implemented as bit-flips in the binary representation of subdomain solutions.
Bound Verification for Soft-Fault Resilience.
 A priori bounds are derived for the discrete solution of second-order, elliptic partial differential equations (PDEs).
The bounds have two contributions. On the one hand, the influence of boundary conditions is taken into account through a discrete maximum principle. On the other hand, the contribution of the source field is evaluated in a fashion similar to that used in the treatment of the continuous a priori operators.
Closed form expressions are in particular obtained for the case of a conservative, second-order finite difference approximation of the diffusion equation with variable scalar diffusivity.
The bounds are then incorporated into a resilient domain decomposition framework, namely to verify the admissibility of local PDE solutions.
The computations demonstrate that the bounds are able to detect most of system faults, and thus considerably enhance the resilience of the solver, as well as its overall performance.
A priori bounds are derived for the discrete solution of second-order, elliptic partial differential equations (PDEs).
The bounds have two contributions. On the one hand, the influence of boundary conditions is taken into account through a discrete maximum principle. On the other hand, the contribution of the source field is evaluated in a fashion similar to that used in the treatment of the continuous a priori operators.
Closed form expressions are in particular obtained for the case of a conservative, second-order finite difference approximation of the diffusion equation with variable scalar diffusivity.
The bounds are then incorporated into a resilient domain decomposition framework, namely to verify the admissibility of local PDE solutions.
The computations demonstrate that the bounds are able to detect most of system faults, and thus considerably enhance the resilience of the solver, as well as its overall performance.
A Resilient Domain Decomposition Polynomial Chaos Solver for Uncertain Elliptic PDEs.
 The resilient method is extended for the solution of uncertain elliptic PDEs on extreme scale platforms.
The method is based on a hybrid domain decomposition, polynomial chaos (PC) framework that is designed to address soft faults.
Specifically, parallel and independent solves of multiple deterministic local problems are used to define PC representations of local Dirichlet boundary-to-boundary maps that are used to reconstruct the global solution.
A LAD-lasso type regression is developed for this purpose.
The performance of the resulting algorithm is tested on an elliptic equation with an uncertain diffusivity field.
Different test cases are considered in order to analyze the impacts of correlation structure of the uncertain diffusivity field, the stochastic resolution, as well as the probability of soft faults.
In particular, the computations demonstrate that, provided sufficiently many samples are generated, the method effectively overcomes the occurrence of soft faults.
The resilient method is extended for the solution of uncertain elliptic PDEs on extreme scale platforms.
The method is based on a hybrid domain decomposition, polynomial chaos (PC) framework that is designed to address soft faults.
Specifically, parallel and independent solves of multiple deterministic local problems are used to define PC representations of local Dirichlet boundary-to-boundary maps that are used to reconstruct the global solution.
A LAD-lasso type regression is developed for this purpose.
The performance of the resulting algorithm is tested on an elliptic equation with an uncertain diffusivity field.
Different test cases are considered in order to analyze the impacts of correlation structure of the uncertain diffusivity field, the stochastic resolution, as well as the probability of soft faults.
In particular, the computations demonstrate that, provided sufficiently many samples are generated, the method effectively overcomes the occurrence of soft faults.
Exascale Implementation.
 The resilient algorithms have been implementated on a server-client model where all state information is held by the servers, while clients are designed solely as computational units.
Scalability tests run up to ~51 K cores show an efficiency greater than 90%.
We use a 2D elliptic PDE and a fault model based on random single bit-flip to demonstrate the resilience
of the application to synthetically injected SDC.
We discuss two fault scenarios: one based on the corruption of all data of a target task,
and the other involving the corruption of a single data point.
We show that for our application, given the test problem considered, the overhead
incurred to overcome the presence of SDC is minimal (less than 7%).
We then discuss potential savings in energy consumption via dynamics voltage/frequency scaling,
and its interplay with fault-rates, and application overhead.
The resilient algorithms have been implementated on a server-client model where all state information is held by the servers, while clients are designed solely as computational units.
Scalability tests run up to ~51 K cores show an efficiency greater than 90%.
We use a 2D elliptic PDE and a fault model based on random single bit-flip to demonstrate the resilience
of the application to synthetically injected SDC.
We discuss two fault scenarios: one based on the corruption of all data of a target task,
and the other involving the corruption of a single data point.
We show that for our application, given the test problem considered, the overhead
incurred to overcome the presence of SDC is minimal (less than 7%).
We then discuss potential savings in energy consumption via dynamics voltage/frequency scaling,
and its interplay with fault-rates, and application overhead.
Domain Decomposition methods for stochastic problems
The work on resilient solvers revealed several interesting features of the domain decomposition approach for the resolution of stochastic partial differential equations. In particular, the idea of sampling over a subdomain the original problem allows to effectively represent its stochastic solution in a reduced (or condensed) format and low-dimensional PC basis. This feature can be exploited to efficiently compute the Karhunen-Loève expansion over spatial domains, a task that is at the root of most stochastic spectral representations of uncertainty. We are currently working on exploiting further the stochastic complexity reduction of the local problems, to accelerate the Monte-Carlo sampling of stochastic elliptic equations.
Parallel Domain Decomposition Method for the of the Karhunen-Loève Expansion.
 In this work we develop a method to efficiently determine the dominant Karhunen-Loève (KL) modes of a random process; more generally, the method solves Fredholm equations of the second kind.
The truncated KL expansion is one of the most common techniques for the approximation of random processes, primarily because it is an optimal representation, in the mean squared error sense, with respect to the number of random variables in the representation. However, finding the KL expansion involves solving integral problems, which tends to be computationally demanding. This work addresses this issue by means of a divide-and-conquer strategy based on a domain decomposition approach, enabling the efficient computation of a possibly large number of dominant KL modes. Specifically, the computational domain is partitioned into smaller non-overlapping subdomains, over which independent local KL decompositions are performed to generate local bases which are subsequently used to discretize the global modes over the entire domain. The latter are determined by means of a Galerkin projection. The procedure leads to the resolution of a reduced Galerkin problem, whose size is not related to the dimension of the underlying discretization space, but is actually determined by the desired accuracy and the number of subdomains. It can also be easily implemented in parallel. Extensive numerical tests are used to validate the methodology and assess its serial and parallel performance.
In this work we develop a method to efficiently determine the dominant Karhunen-Loève (KL) modes of a random process; more generally, the method solves Fredholm equations of the second kind.
The truncated KL expansion is one of the most common techniques for the approximation of random processes, primarily because it is an optimal representation, in the mean squared error sense, with respect to the number of random variables in the representation. However, finding the KL expansion involves solving integral problems, which tends to be computationally demanding. This work addresses this issue by means of a divide-and-conquer strategy based on a domain decomposition approach, enabling the efficient computation of a possibly large number of dominant KL modes. Specifically, the computational domain is partitioned into smaller non-overlapping subdomains, over which independent local KL decompositions are performed to generate local bases which are subsequently used to discretize the global modes over the entire domain. The latter are determined by means of a Galerkin projection. The procedure leads to the resolution of a reduced Galerkin problem, whose size is not related to the dimension of the underlying discretization space, but is actually determined by the desired accuracy and the number of subdomains. It can also be easily implemented in parallel. Extensive numerical tests are used to validate the methodology and assess its serial and parallel performance.
PC acceleration of Domain Decomposition based Monte Carlo method for Elliptic PDEs.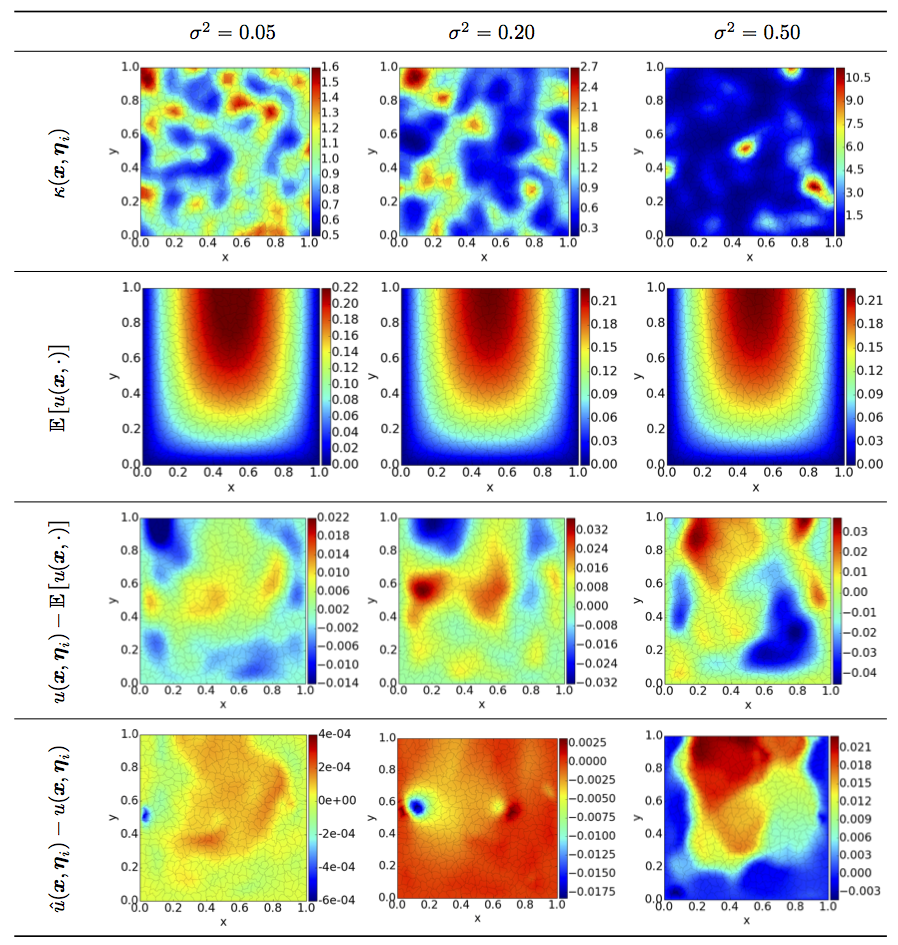 The local expansion of the diffusivity fields at the level of a subdomain, using few local random variables, suggests the possibility of locally expanding the elliptic solution using a low dimensional PC basis. Unfortunately, this is not feasible because the boundary values of a subdomain usually involve dependences with respect to all other subdomains and their associated random variables.
Still, decomposition the reduced problem for all subdomains boundary unknowns as a sum of contributions from the subdomains, we show that these elementary contributions can be expanded using low dimensional PC basis. This possibility is exploited to accelerate the Monte Carlo procedure to generate efficiently samples of the stochastic solution.
We propose a fully parallel method where PC approximations of the subdomain contributions to the boundary-to boundary maps are first computed in a preprocessing stage. Then, in the sampling stage, local random variables parameterizing the diffusivity field are jointly sampled to generate approximate condensed problem which are subsequently solved to obtain samples of the solution. The acceleration comes from the need of reconstructing for each samples the boundary-to-boundary maps, or solving multiple local problems if an iterative solver is considered. The scalability of the method is also investigated.
The local expansion of the diffusivity fields at the level of a subdomain, using few local random variables, suggests the possibility of locally expanding the elliptic solution using a low dimensional PC basis. Unfortunately, this is not feasible because the boundary values of a subdomain usually involve dependences with respect to all other subdomains and their associated random variables.
Still, decomposition the reduced problem for all subdomains boundary unknowns as a sum of contributions from the subdomains, we show that these elementary contributions can be expanded using low dimensional PC basis. This possibility is exploited to accelerate the Monte Carlo procedure to generate efficiently samples of the stochastic solution.
We propose a fully parallel method where PC approximations of the subdomain contributions to the boundary-to boundary maps are first computed in a preprocessing stage. Then, in the sampling stage, local random variables parameterizing the diffusivity field are jointly sampled to generate approximate condensed problem which are subsequently solved to obtain samples of the solution. The acceleration comes from the need of reconstructing for each samples the boundary-to-boundary maps, or solving multiple local problems if an iterative solver is considered. The scalability of the method is also investigated.
 In this work we develop a method to efficiently determine the dominant Karhunen-Loève (KL) modes of a random process; more generally, the method solves Fredholm equations of the second kind.
The truncated KL expansion is one of the most common techniques for the approximation of random processes, primarily because it is an optimal representation, in the mean squared error sense, with respect to the number of random variables in the representation. However, finding the KL expansion involves solving integral problems, which tends to be computationally demanding. This work addresses this issue by means of a divide-and-conquer strategy based on a domain decomposition approach, enabling the efficient computation of a possibly large number of dominant KL modes. Specifically, the computational domain is partitioned into smaller non-overlapping subdomains, over which independent local KL decompositions are performed to generate local bases which are subsequently used to discretize the global modes over the entire domain. The latter are determined by means of a Galerkin projection. The procedure leads to the resolution of a reduced Galerkin problem, whose size is not related to the dimension of the underlying discretization space, but is actually determined by the desired accuracy and the number of subdomains. It can also be easily implemented in parallel. Extensive numerical tests are used to validate the methodology and assess its serial and parallel performance.
In this work we develop a method to efficiently determine the dominant Karhunen-Loève (KL) modes of a random process; more generally, the method solves Fredholm equations of the second kind.
The truncated KL expansion is one of the most common techniques for the approximation of random processes, primarily because it is an optimal representation, in the mean squared error sense, with respect to the number of random variables in the representation. However, finding the KL expansion involves solving integral problems, which tends to be computationally demanding. This work addresses this issue by means of a divide-and-conquer strategy based on a domain decomposition approach, enabling the efficient computation of a possibly large number of dominant KL modes. Specifically, the computational domain is partitioned into smaller non-overlapping subdomains, over which independent local KL decompositions are performed to generate local bases which are subsequently used to discretize the global modes over the entire domain. The latter are determined by means of a Galerkin projection. The procedure leads to the resolution of a reduced Galerkin problem, whose size is not related to the dimension of the underlying discretization space, but is actually determined by the desired accuracy and the number of subdomains. It can also be easily implemented in parallel. Extensive numerical tests are used to validate the methodology and assess its serial and parallel performance.
PC acceleration of Domain Decomposition based Monte Carlo method for Elliptic PDEs.
 The local expansion of the diffusivity fields at the level of a subdomain, using few local random variables, suggests the possibility of locally expanding the elliptic solution using a low dimensional PC basis. Unfortunately, this is not feasible because the boundary values of a subdomain usually involve dependences with respect to all other subdomains and their associated random variables.
Still, decomposition the reduced problem for all subdomains boundary unknowns as a sum of contributions from the subdomains, we show that these elementary contributions can be expanded using low dimensional PC basis. This possibility is exploited to accelerate the Monte Carlo procedure to generate efficiently samples of the stochastic solution.
We propose a fully parallel method where PC approximations of the subdomain contributions to the boundary-to boundary maps are first computed in a preprocessing stage. Then, in the sampling stage, local random variables parameterizing the diffusivity field are jointly sampled to generate approximate condensed problem which are subsequently solved to obtain samples of the solution. The acceleration comes from the need of reconstructing for each samples the boundary-to-boundary maps, or solving multiple local problems if an iterative solver is considered. The scalability of the method is also investigated.
The local expansion of the diffusivity fields at the level of a subdomain, using few local random variables, suggests the possibility of locally expanding the elliptic solution using a low dimensional PC basis. Unfortunately, this is not feasible because the boundary values of a subdomain usually involve dependences with respect to all other subdomains and their associated random variables.
Still, decomposition the reduced problem for all subdomains boundary unknowns as a sum of contributions from the subdomains, we show that these elementary contributions can be expanded using low dimensional PC basis. This possibility is exploited to accelerate the Monte Carlo procedure to generate efficiently samples of the stochastic solution.
We propose a fully parallel method where PC approximations of the subdomain contributions to the boundary-to boundary maps are first computed in a preprocessing stage. Then, in the sampling stage, local random variables parameterizing the diffusivity field are jointly sampled to generate approximate condensed problem which are subsequently solved to obtain samples of the solution. The acceleration comes from the need of reconstructing for each samples the boundary-to-boundary maps, or solving multiple local problems if an iterative solver is considered. The scalability of the method is also investigated.
Contact



Cell: +33 (0) 614 800 420
olivier.le-maitre"at"polytechnique.edu
CMAP
Ecole Polytechnique
route de Saclay
91128 Palaiseau cedex, France
olivier.le-maitre"at"polytechnique.edu
CMAP
Ecole Polytechnique
route de Saclay
91128 Palaiseau cedex, France